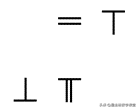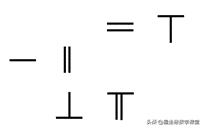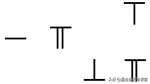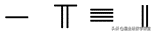学数学，就上星坐标！你好，这里是星坐标头条。

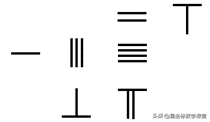
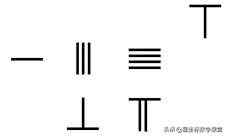
在上一期的头条节目中，我为你介绍了算筹记数的方法，那么，完成了记数，肯定还是要进行计算的。那算筹又是怎样来计算的呢？今天我们就来具体地聊一聊。

我们以加法和乘法为例来进行说明，同时，建议你结合加法、乘法的竖式计算，看看都有哪些发现。

本期内容图片比较多，为了便于理解，建议你对照着文稿来听，效果可能会更好一些。

用算筹做加法

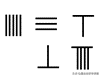
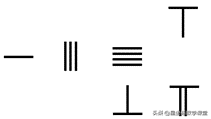
我们先来演示一下用算筹进行加法运算。以536+69为例：

第一步：将加数536放在第一行，另一个加数69放在第二行，同时要保证每个加数的各个数位对齐。接着，我们从左到右将各个数位上的数字相加。

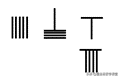
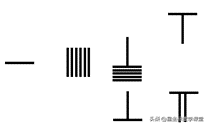
第二步：将第二行十位上的1根竖棍和1根横棍移到第一行的十位上。

第三步：将第二行个位上的1根横棍和4根竖棍移到第一行的个位上。

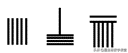
第四步：此时，第一行的个位上出现了2根横棍，个位数超过了10。因此，去掉其中的2根横棍，同时在十位上添加1根横棍。

第五步：第一行的十位上有了1根竖棍，5根横棍，正好是10。因此，把它们全部去掉，同时在百位上添加1根竖棍。此时十位上为0，按照规定，十位就要空出来。

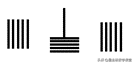
第六步：第一行百位上的竖棍个数超过了5，把其种5根竖棍换成1根横棍。

这样，就得到了最终结果是：536+69=605。

用算筹做乘法

接下来，我们再演示一下用算筹进行乘法运算。以26×67为例。

第一步：将被乘数26放在第一行，乘数67放在第三行。因为没有运算符号，为了跟前面的加法区分开来，所以将下行的数往左移动一格，使乘数的个位对齐被乘数的最高位。而第二行先空着，用来放计算结果。接下来，用第一行的每一位数分别乘第三行的每一位数。

第二步：用第一行十位上的2乘第三行十位上的6。根据九九乘法表，2×6=12。将12放在第二行，个位对齐第三行十位上的6。

第三步：用第一行十位上的2乘第三行个位上的7。根据九九乘法表，2×7=14。将14添加到第二行里，个位对齐第三行个位上的7。

第四步，此时，第一行十位上的2已经乘遍了第三行的每一位数。因此，将第一行十位上的2拿走。

第五步：将第三行整体右移一格。

第六步：用第一行个位上的6乘第三行十位上的6。根据九九乘法表，6×6=36。将36添加到第二行里，个位对齐第三行十位上的6。

第七步：第二行当前的末位上有1根竖棍，5根横棍，正好是10。因此，把它们全部去掉，同时在前一位上添加1根竖棍。

第八步：第二行当前的末位上的竖棍个数超过了5，把其中5根竖棍换成1根横棍。

第九步：用第一行个位上的6乘第三行个位上的7。将42添加到第二行里，个位对齐第三行个位上的7。

第十步：此时，第一行个位上的6也已经乘遍了第三行的每一位数。因此，将第一行和第三行的数全部拿走，剩下的就是乘法算式的得数。所以，最终我们得到，26×67=1742。

算筹和竖式对比

通过以上的计算，你有没有发现，其实算筹的计算方法是非常有趣的。那么，对比我们现在所使用的竖式计算，你有什么发现呢？实际上，竖式和算筹在算法上既有相同点，也有不同点。不同点是，算筹是从上往下算，竖式是从下往上算，算筹是高位算到低位，竖式是从低位算到高位。但是，它们的道理是一样的。

算筹记数法的历史意义

与其它古代文明相比较，算筹记数的思想是古代中国独创的、是最有效的计算工具。虽说算筹也有不足之处，比如运算时占地方大、用筹多、取用麻烦、难免碰动，很容易引起差错，并且，它于15世纪被算盘所取代。可尽管如此，算筹记数法依然是最早将十进制和位值制二者结合在一起使用的记数方法，马克思还称“十进位值制记数法”是“最妙的发明之一”。

相信通过昨天和今天两期节目，你对算筹一定有了全新的认识，那么请你思考这样一个问题：对于下面这个乘法算式：78×56，你能否用算筹的方法进行计算呢？

欢迎你在评论区留言互动，分享你的看法。

以上就是今天的头条内容，希望听了以后对你有所启发，我们明天再见！